피보나치 수열
: 처음 두 항을 1과 1로 정하고, 그 다음 항부터는 앞의 두 개의 항을 더해 만드는 수열
1 , 1 , 2 , 3 , 4 , 5 , 13 , 21 , 34 , 55 , · · ·
이 수열에 속한 수를 피보나치 수라고 한다.
- f(0) = 0 으로 시작하기도 함
- 첫 번째 피보나치 수 f(1) = 1
- 두 번째 피보나치 수 f(2) = 1
- 세 번째 피보나치 수 f(3) = f(2) + f(1) = 2
- 네 번째 피보나치 수 f(4) = f(3) + f(2) = 3
- n 번째 피보나치 수 f(n) = f(n-1) + f(n-2)
▶ n 번째 피보나치 수 구하는 코드 만들어보기
def fibonacci(n): # 함수정의, 결과는 n번째 피보나치 수
if n == 1 or n == 2: # 수열의 1, 2번째 값은
return 1 # 1임.
else: # 3번째 부터는
return fibonacci(n-1) + fibonacci(n-2) # 이전 두 항의 합
print(fibonacci(10)) # 55 # 피보나치 수열의 10번째 수
▶ 코드 흐름도

재귀호출을 계속 타고 들어가다가 return을 만나면
본인이 호출되었던 위치(화살표 역방향)로 다시 돌아와서
본인의 오른쪽에 남아있는 코드를 마저 실행한다.

근데 흐름을 잘 보면 똑같은 부분을 반복하고 있는 부분이 보인다.(초록네모)
같은 계산을 처음부터 일일이 다시하고있다... 매우 비효율적
n이 큰 수라면 시간이 굉장히 오래 걸릴 것이다.
실제로 100번째 피보나치 수 계산을 실행해보면,

계속 기다렸는데 결과가 안나옴
그리고 컴퓨터도 위이이ㅔㅇ엥 소리가 커지면서 짜증낸다..
짜증만 내고 결과는 안나옴
이걸 방지하기 위해서 이미 계산한 값은 '메모' 해뒀다가 꺼내 쓰는 방법이 있다.
메모이제이션(Menoization)
: 중복 계산을 피하기 위해 결과를 저장하고 재사용하는 최적화 방법
- 계산한 값을 저장할 공간을 마련(배열, 딕셔너리 등)
- 재귀호출 하기 전에 이미 해당 값이 저장되어 있는지 확인
- 저장되어 있다면 재귀호출 대신 그 값을 사용
- 저장된 값이 없다면 재귀호출로 값 계산 후, 계산결과를 저장소에 저장
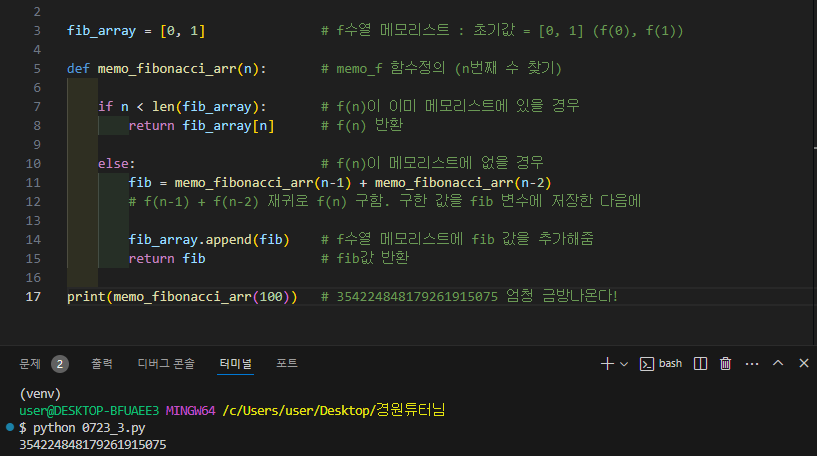
▶ 메모이제이션_리스트 코드
fib_array = [0, 1] # f수열 메모리스트 : 초기값 = [0, 1] (f(0), f(1))
def memo_fibonacci_arr(n): # memo_f 함수정의 (n번째 수 찾기)
if n < len(fib_array): # f(n)이 이미 메모리스트에 있을 경우
return fib_array[n] # f(n) 반환
else: # f(n)이 메모리스트에 없을 경우
fib = memo_fibonacci_arr(n-1) + memo_fibonacci_arr(n-2)
# f(n-1) + f(n-2) 재귀로 f(n) 구함. 구한 값을 fib 변수에 저장한 다음에
fib_array.append(fib) # f수열 메모리스트에 fib 값을 추가해줌
return fib # fib값 반환
print(memo_fibonacci_arr(100)) # 354224848179261915075 엄청 금방나온다!
▶ 코드 흐름도

처음엔 메모 공간에 f(0), f(1) 값만 있지만
f(n)값을 새로 계산 해낼 때마다 메모 공간에 저장해줌!
따라서 다음에 똑같은 재귀함수가 등장했을 경우 계산 다시 안해도 된다. 오예!
메모이제이션 방법으로 100번째 피보나치 수 계산을 실행해보면,
이번엔 안기다려도 바로 대답해준다! 완전 신기
컴퓨터가 소리 짜증도 안냄
메모 [리스트] 말고 메모 {딕셔너리} 형태도 가능하다.
▶ 메모이제이션_딕셔너리 코드
def fibonacci(n, memo={}): # f함수선언 (n받기, memo를 딕셔너리로 지정함으로써 앞으로 memo 변수에 '업데이트' 기능을 쓸 수 있게 해준다.)
if n in memo: # memo 딕셔너리의 key값에 n이 있다면,
return memo[n] # 해당 key의 value값(=f(n))을 반환한다.
if n <= 1: # memo 딕셔너리의 key값에 n이 없지만, n이 0 또는 1 이라면,
return n # n을 그대로 반환한다. 즉, f(0)=0, f(1)=1 이라는 기저조건 생성.
memo[n] = fibonacci(n - 1, memo) + fibonacci(n - 2, memo)
# memo 딕셔너리 안에 f(n)도 없고, n이 0이나 1도 아니라면,
# 앞의 두항을 더해서 f(n)값을 계산한다.
# 그 값을 memo 딕셔너리에, n(key) : f(n)(value) 형태로 업데이트 해준다.
return memo[n]
# 그 후에 memo[n]을 반환한다.
# dictionary[key] 형태이므로, n(key)에 해당하는 f(n)(value)이 반환된다.
# i가 0부터 9까지에 각각 위의 함수를 호출해서 return한 값을 출력한다.
for i in range(10):
print(f"Fibonacci({i}) = {fibonacci(i)}")
# Fibonacci(0) = 0
# Fibonacci(1) = 1
# Fibonacci(2) = 1
# Fibonacci(3) = 2
# Fibonacci(4) = 3
# Fibonacci(5) = 5
# Fibonacci(6) = 8
# Fibonacci(7) = 13
# Fibonacci(8) = 21
# Fibonacci(9) = 34
중복계산을 하지 않으니 겁나 빠르다.
이렇게 하나의 문제를 작은 하위 문제들로 나누고, 각 하위 문제를 한 번씩만 해결하여 저장한 후에 최종 문제를 해결하는 방식을 '동적 계획법(DP)' 이라고 한다.
DP에는 상향식(Bottom-up) 접근 방식과 하향식(Top-Down) 접근 방식이 있는데, 메모이제이션은 DP의 하향식 접근 방식에 해당함.
▶ 재귀함수 (Recursive Function)
: 문제에서 같은 계산이 반복적으로 필요할 때 재귀적으로 해결함.
▶ 메모이제이션 (Memoization)
: DP 중 하나. 계산된 값을 저장함으로써 중복 계산을 피해 재귀함수를 최적화함.
▶ 동적 계획법 (Dynamic Programming, DP)
: 문제를 하위 문제들로 나눈 후, 해결 결과를 저장하여 최종 결과를 얻음.
'알고리즘&자료구조' 카테고리의 다른 글
| [알고리즘] 선택 정렬, 삽입 정렬 (0) | 2024.07.25 |
|---|---|
| [알고리즘] 선택정렬, 삽입정렬코드 (0) | 2024.07.24 |
| [알고리즘] 재귀함수 (0) | 2024.07.23 |
| [알고리즘] 중첩 for문 문제 (0) | 2024.07.22 |
| [알고리즘] 버블 정렬(Bubble Sort) (0) | 2024.07.19 |